26. 抗量子多方安全计算
26.1. 需求背景
本模块为长安链提供一种抗量子的多方门限解密能力,加密方使用公钥对数据进行加密,多个私钥持有方联合对数据进行解密。
在区块链应用场景中,常常需要有大量隐私数据存储,为了保护数据的隐私,数据往往以加密的形式进行存储。但解密用的私钥如果在单个节点上进行管理,会造成节点权限过大和私钥泄露风险。
抗量子多方门限解密可以使得私钥由多个节点进行管理,需要对加密数据进行解密的时候,对多个私钥管理节点发起解密请求,私钥管理节点使用自己的私钥份额对数据执行解密,得到解密分片,将解密分片发送给解密请求方,解密请求方收集到一定数量的解密分片后,恢复出隐私数据。
传统多方门限解密的构造都依赖于大整数分解、离散对数求解等困难问题,然而在量子计算机的攻击下,这些困难问题将不再安全。基于格构造的密码算法通常依赖于格上的困难问题,如格上最短向量问题、最近向量问题,这些困难问题在量子计算机攻击下仍然是安全的。在众多基于格构造的密码算法中,基于NTRU格构造的算法具有输出向量短,运算高效的特性,本模块研究基于NTRU格的多方门限解密算法,利用线性秘密分享方案对私钥进行安全切割。
了解使用方法,请参考抗量子多方安全计算使用文档
26.2. 场景介绍
在业务场景中,某份敏感数据加密给董事会,用于汇报,由于数据敏感性,需要多个董事会成员在场,数据才能被解密。
医疗数据库中,病人的敏感数据通常加密存储,使用单私钥解密会使得私钥掌管方权限过大,切一旦私钥泄露,则会造成隐私数据泄露。通过多方门限解密,可以将私钥的解密能力分散给各个数据库监督管理节点,只有多个节点联合解密,请求数据方才能获得敏感数据。
26.3. 实施方案
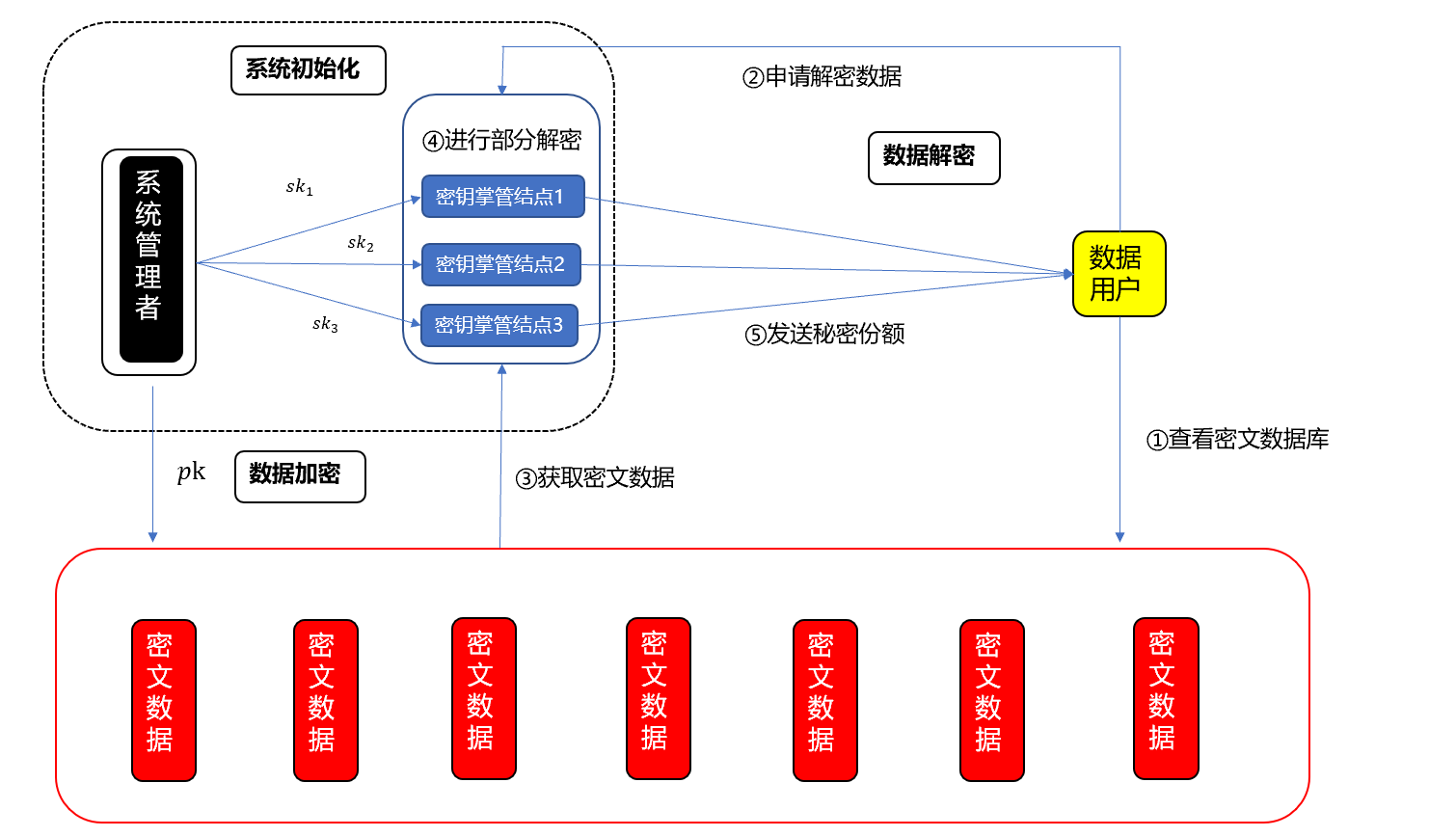
长安链系统初始化后,将NTRU算法的私钥按(t-n)门限切割后分发给数据管理节点进行掌管。将公钥在系统内进行公开
业务数据方使用公钥对隐私数据进行加密存储
数据用户进行解密申请
数据用户通过智能合约向密钥掌管节点申请解密密文数据
密钥掌管节点执行部分解密得到解密分片
密钥掌管节点将解密分片发送给数据用户
数据用户收集到一定数量的解密分片后,执行最终解密。
整体架构如图所示
26.4. 长安链的抗量子多方安全门限算法介绍
26.4.1. 线性秘密分享方案
长安链的抗量子多方安全门限算法使用的线性秘密分享方案基于Dan Boneh等人于2018年提出的{0,1}-LSSS 方案,具体的细节为
(1) 首先对于一般的t/u门限方案,其对应的布尔表达式为析取范式 $\bigvee{(\bigwedge{P_i)}}$,其中$P_i$为第$i$个密钥掌管结点,这种特殊形式的布尔表达式中只包含“与”和“或”,因此是单调的布尔表达式,我们可以根据该布尔表达式构造一个二叉树结构,其叶子结点为表达式中的全部$P_i$,非叶子结点为两个子树对应表达式之间的“与”或者“或”,最后从树的根结点出发即可还原整个布尔表达式。
(2) 对上面得到的二叉树使用Folklore算法,详细过程如下:
a. 为根结点赋值$m_1=(1)$,令count=1;
b. 对表达式形成的树上的每个结点n执行如下操作:
若结点n对应“或”,则将结点n的值m赋给左右孩子;
若结点n对应“与”,则在m的末尾补0,使得m的长度等于count,然后在m的后面补一个1并将其赋值给左孩子,最后将长为count+1的向量$(0,0,\ldots,0,-1)$赋给右孩子,并令count=count+1;
c. 取出所有叶子结点的值,并在这些值后面补0使得他们的长度相同。
(3) 对将得到的所有叶子结点的值按照顺序排成一列,构成一个$t\cdot C_u^t\ \times\ \left(t-1\right)\cdot C_u^t+1$的矩阵,该矩阵即为秘密分享矩阵M。
(4) 为了得到私钥k对应的每个密钥掌管结点的秘密份额,首先在$Z_p$上按照离散高斯分布采样得到随机数$r_2,r_3,\ldots,r_n$,然后定义向量$w=M\cdot\left(k,r_2,r_3,\ldots,r_n\right)^T$,此时长为$t\cdot C_u^t$的列向量w中的每个数字即为对应密钥掌管结点$P_i$在进行秘密分享时的一个秘密份额。
26.5. 抗量子多方门限加密方案
长安链的抗量子多方门限加密方案基于NTRU加密算法[2]构造,方案包含以下三个公共参数:正整数$N$,对应多项式的次数;大模数$q$和小模数$p$,满足$\left(q,p\right)=1$,且$q\gg p$,在方案中我们取$p=3$。此外,我们还需要定义多项式环$\mathcal{R}=Z\left[x\right]/(X^N-1)$。
抗量子多方门限加密方案的密钥生成过程如下:
首先任取多项式$F,G$,满足$F,G$的系数均属于${-1,0,1}$;
令$f\ =\ 1+pF$, 如果$f$在多项式环$\mathcal{R}_q$上不可逆,则重新选择多项式
令$g=pG$,定义$h=f^{-1}g\ mod\ q$
对于(t-n)门限,按线性秘密分享方案构造秘密分享矩阵shareMatrix,初始一条长度为shareMatrix列数的向量k,设置$k\left[0\right]=f$,其余分量按步骤(1)、(2),生成$f_1,f_2,\ldots$,并设置$k\left[1\right]=f_1,k\left[2\right]=f_2,…$
令$keys\ =\ shareMatrix\ \cdot k$,将$keys$各分量分给各参与方
输出公钥为$h$,私钥份额$keys$
抗量子多方门限加密方案的加密过程如下:
任取随机多项式$r$;
对于明文消息$m$,计算密文$y=r\ast h+m\ (mod\ q)$。
部分解密过程如下:
门限值t个参与方进行解密
各个参与方计算$a_i=f_i\ast y\left(mod\ q\right)$
最终解密过程如下:
计算$a\ =\ \sum a_i\left(mod\ q\right)$
明文$m=\ a(mod\ p)$
26.6. 函数说明
26.6.1. 相关结构体
26.6.1.1. PublicKey
type PublicKey struct {
H *poly.Polynomial
}
PublicKey结构体存储公钥信息,H为公钥多项式
26.6.1.2. PrivateKey
type PrivateKey struct {
PublicKey
F *poly.Polynomial
}
PrivateKey 结构体存储私钥信息,包括匹配的公钥、私钥对应多项式。
26.6.2. 相关函数
26.6.2.1. Public
func (priv *PrivateKey) Public() *PublicKey
私钥获取对应公钥。
26.6.2.2. Encrypt
func (pub *PublicKey) Encrypt(rand io.Reader, plain *poly.Polynomial) (cipher *poly.Polynomial, err error)
公钥加密原多项式,生成加密多项式,rand 为随机源,plain 为原多项式,cipher 为加密后的多项式。
26.6.2.3. Decrypt
func (priv *PrivateKey) Decrypt(cipher*poly.Polynomial) (plain *poly.Polynomial)
使用私钥对加密多项式进行解密。cipher 为加密多项式,plain 为解密后的多项式。
26.6.2.4. GenerateKey
func GenerateKey(rand io.Reader) (privateKey *PrivateKey, err error)
根据随机源生成公私钥对,rand 为随机源,privateKey 为生成的私钥,内包含公钥
26.6.2.5. GenerateThresholdKey
GenerateThresholdKey(rand io.Reader, threshold, total int64) (privateKeys []*PrivateKey, err error)
生成门限算法秘密分享的多个公私钥对,rand 为随机源,threshold 为门限值,total 为生成的总密钥数量,privateKeys 为生成的多个密钥
26.7. 正确性验证
在 ntru_test.go 文件中对密钥生成、加密、解密进行了正确性验证。
26.8. 参考文献
[1] Boneh D, Gennaro R, Goldfeder S, et al. Threshold cryptosystems from threshold fully homomorphic encryption[C]//Annual International Cryptology Conference. Springer, Cham, 2018: 565-596.
[2] Hoffstein J, Pipher J, Silverman J H. NTRU: A ring-based public key cryptosystem[C]//International algorithmic number theory symposium. Springer, Berlin, Heidelberg, 1998: 267-288.