长安链 Bulletproofs 零知识证明方案设计文档
需求
需求概述
在目前主流的公链上,诸如比特币、以太坊,从创世块开始,每个账号之间的交易信息都是被公开记录在区块链上的,所以雇员并不喜欢被用bitcoin来支付薪水,因为那样他们的薪水金额将发布到公链上。为了解决交易金额的机密性,Maxwell 在2016年《Confidential transactions》提出了confidential transactions (CT) 概念,通过对每笔交易金额进行commit实现隐藏。CT所面临的一个困难是它会把交易体积变得很大而且验证速度很慢,因为CT需要每一笔交易输出都含有一个范围证明(range proofs)。同时具有短证明长度和不需要可信初始化设置的Bulletproofs零知识证明方案,尤其适合用于为committed values提供range proofs。
具体场景
隐私交易,隐藏交易金额,可以进行金额的数值范围判断。
Bulletproofs零知识证明
Bulletproofs 概述
Benedikt B¨unz、 Jonathan Bootle和 Dan Boneh等人2018年论文《Bulletproofs: Short Proofs for Confidential Transactions and More》中提出了Bulletproofs,一个新的零知识证明协议。
零知识证明指的是证明者能够在不向验证者提供任何有用的信息的情况下,使验证者相信某个论断是正确的。零知识证明实质上是一种涉及两方或更多方的协议,即两方或更多方完成一项任务所需采取的一系列步骤。证明者向验证者证明并使其相信自己知道或拥有某一消息,但证明过程不能向验证者泄漏任何关于被证明消息的信息。
零知识证明具有三个特性:零知识、完备性和公正性。
零知识:通过给出的证明、验证过程及公共信息,无法计算出证明中包含的隐藏命题组件。
完备性:按算法制作的对正确命题的证明都能通过验证。
公正性:由不正确的命题生成的证明无法通过验证。
零知识范围证明是机密交易系统的最关键的组成部分,范围证明允许验证者确保秘密值(例如资产金额)是非负的。 这可以防止用户赊账。 由于每项交易涉及一个或多个范围证明,因此它们的效率在证明尺寸和验证时间方面都是交易性能的关键。
建立在Bootle等人的技术基础上,基于离散对数假设,采用了Fiat-Shamir变换实现了从交互式到非交互式的零知识证明,是一种更加空间高效的零知识证明的形式。Pedersen commitments和公钥的原生支持。这让我们可以在通用的零知识框架下实现诸如rangeproofs之类的功能,而不用在零知识中实现复杂的椭圆曲线算法。
和Bootle的range proofs相比较,Bulletproofs证明的输出范围从\([0,2^{32})\)扩大到了\([0,2^{64})\),即使范围扩大了一倍,但是证明的字节大小也仅仅增加了64字节,同时验证的速度也变快了并且支持批量的验证。
Bulletproofs比范围证明更普遍一些,它可以用于在零知识中证明任意陈述。Bulletproofs的证明类似于SNARK或STARK,但可以原生支持椭圆曲线(EC)公钥和Pedersen承诺。
总结:
类似于SNARKs或者STARKs,Bulletproofs是一个一般性的零知识证明
可用来拓展多方协议,比如说多重签名。
提供更高效的及加密交易的范围证明。
这些范围证明可以在交易内进行聚合,大小呈指数增长。
零知识证明研究现状
假设在一个特定场景中,有函数 \(f(x)=y\) ,A告诉B说他知道x是什么,但是A又不想透露x的信息,x可能是A花费了很多资源代价才得到的,这时候A就可以使用零知识算法,生成一个零知识证明 π 而不用暴露原来x的信息。B对π进行认证,来确认A是否真的知道满足函数f的x。例如,在范围证明中,x可有类比为已知数的范围,输出y为1或0(true or false)。
我们可以从以下几个方面来对生成零知识的算法的优劣进行分析:
•生成”π”的时间复杂度
•”π”的大小
•认证”π”的时间复杂度
•需不需要trusted setup
显然,生成,验证”π”的时间复杂度和”π”的大小越小越好,不需要生成可信设置可以减少信任问题和安全问题。
不同零知识证明系统的比较:
Proof system |
Σ Protocal |
SNARKS |
STARKs/CS-Proofs |
Bulletproofs |
|---|---|---|---|---|
Proof size |
long |
short |
shortish |
short |
Prover |
linear |
fft |
fft(big memort req.) |
linear |
Verfier |
linear |
efficient |
efficient |
linear |
Trusted Setup |
no |
required |
no |
no |
Practial |
yes |
yes |
not quite |
yes |
Assumptions |
discrete-log |
non-falsifiable |
owf(quantum secure) |
discrete-log |
通过比较发现,Bulletproofs优秀于Σ Protocal,和zk-snark相比,它不需要可信设置;和zk-stark算法相比,它具有较小的proof size。
Bulletproofs在长安链中的应用
算法构造
首先介绍承诺算法。
数字承诺是指发送方暂时以隐藏的方式向接收方承诺一个值,承诺后不能再对该值做出任何修改。承诺算法由两部分组成:
第一步:承诺,发送方将一个消息锁进盒子中,再将该盒发送给接收方。
第二步:展示,发送方打开盒,向接收方展示盒中的内容。
隐藏性:上述步骤一完成后,接收者无法获得发送者所承诺承诺的值。
捆绑性:上述步骤二完成后,发送者只能向接收者展示一个值。
承诺的隐藏性可以为链上数据提供隐私保护,而捆绑性则可以为保密数据的链上公开监管提供保障。
Pedersen承诺算法详情
Pedersen承诺是基于椭圆曲线离散对数困难假设的。
pedersen承诺的公式为:\(C=x\cdot G+r\cdot H \) 和 \(H\) 为椭圆曲线上的随机点作为公共参数。
隐藏性:指定一个承诺 \(C\) ,无法算出其中绑定的数值 \(x\) 。
捆绑性:给出一个承诺\(C\)及其绑定的数值和致盲因子对\((x,r)\)使得 \(Open(c,x,r)\rightarrow true\) ,无法找到另一组 \((x,r)\ne (x',r')\)使得\(Open(c,x',r')\rightarrow true\) 。
Pedersen承诺产生方式,有些类似加密,签名之类的算法。但是,作为密码学承诺重在“承诺”,并不提供解密算法,即如果只有\(r\),无法有效地计算出原始数据 \(x\) 。
Pedersen承诺的加法同态性
两个承诺 \(C(x)=x\cdot G+r_1\cdot H \)的承诺结果为
\(C(x+y)=(x+y)\cdot G +(r_1+r_2)\cdot H =(x\cdot G+r_1\cdot H) +(y\cdot G+r_2\cdot H)=C_x+C_y\)
Pedersen承诺是一个强有力的密码学工具,数据以承诺的形式上链,用于隐藏交易数额,同时又通过捆绑性来防止伪造篡改交易金额。
于是我们就利用Pedersen算法的同态性在链上进行交易。但这样做会有一个问题,比如说在一个特定场景中,我们需要规定转账的金额大于账户余额,这时候就需要用到零知识范围证明了。
在Bulletproofs零知识范围证明中,要证明的基本命题是数值 \(x\in[0,2^{64})\) ,其中\(x\)是不公开的秘密,。
公共信息: \(G,H\) \(C=x\cdot G+r\cdot H\)
证明者的秘密输入: \(x\in[0,2^{64}),r\)
验证者和证明者在 Σ Protocol协议框架下进行多轮交互,最后验证了承诺中的 \(C\) 与 初始数值\(x\) 是绑定的以及x在\([0,2^{64})\)范围内。
下面是秘密信息x,x的opening,x的commitment,x的proof的运算表;commitment由秘密信息x和致盲因子opening唯一确定,proof的生成引入了随机数,每次生成的proof不一定相等但是都可以用来证明。
x |
opening_x |
commitment_x |
proof_x |
|---|---|---|---|
运算 |
opening |
commitment |
proof |
x + a |
opening_x |
commitment_(x + a) |
proof_(x + a) |
x + y |
opening_x + opening_y |
commitment_x + commitment_y |
proof(x+y) |
x - a |
opening_x |
commitment_(x - a) |
proof_(x - a) |
x - y |
opening_x - opening_y |
commitment_x - commitment_y |
proof(x-y) |
x * a |
opening_x * a |
commitment_x * a |
proof_(x * a) |
方案描述
整体架构
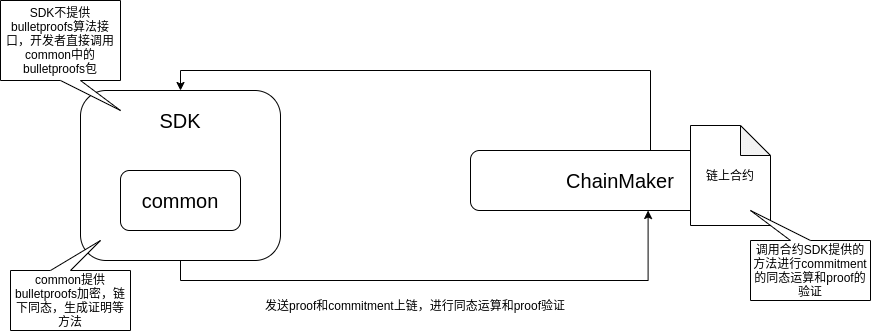
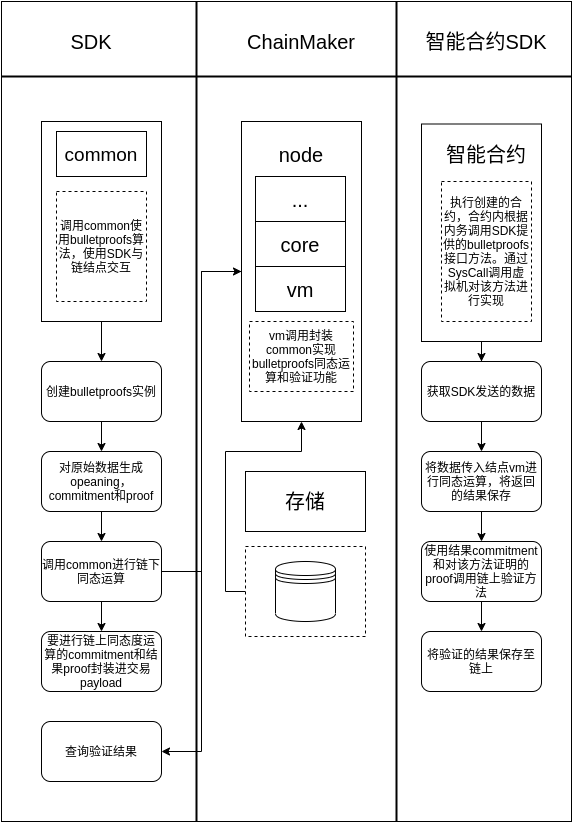
执行流程
[1]Benedikt B¨unz, Jonathan Bootle, Dan Boneh, Andrew Poelstra, Pieter Wuille, and Greg Maxwell. Bulletproofs: Short proofs for confidential transactions and more (conference version). In Security and Privacy (SP), 2018 IEEE Symposium on, pages 319–338. IEEE, 2018.
[2]Oleg Andreev. Hidden in Plain Sight: Transacting Privately on a Blockchain. blog.chain.com, 2017.
[3] On the Size of Pairing-based Non-interactive Arguments? JensGroth University College London,UKj.groth@ucl.ac.uk
[4]Elli Androulaki, Ghassan O Karame, Marc Roeschlin, Tobias Scherer, and Srdjan Capkun. Evaluating User Privacy in Bitcoin. In Financial Cryptography, 2013.
[5]Jonathan Bootle, Andrea Cerulli, Pyrros Chaidos, Jens Groth, and Christophe Petit. Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 327–357. Springer, 2016.
[6]G Dagher, B B¨unz, Joseph Bonneau, Jeremy Clark, and D Boneh. Provisions:Privacy-preserving proofs of solvency for bitcoin exchanges (full version). Technical report, IACR Cryptology ePrint Archive, 2015.