长安链同态加密方案设计文档
背景
需求
需求概述
在互联网技术不断成熟完善的今天,为了保护用户隐私,数据往往以密文的形式在计算机内进行存储。但是,密文形式的数据难以计算、处理的特性从某种程度上来说限制了诸如云计算、匿名投票等许多应用。同态加密作为解决该问题的有效手段得到了迅速的发展。同态加密除了能实现传统的数据加密之外,还可以保证密文操作与明文操作对应,从根本上解决了加密数据不可操作性的问题。Paillier 算法就是一种具有良好同态特性的加密算法,在需要密文加法计算、密文明文乘法计算的场合极具竞争力。总而言之,同态加密提供了一种对加密数据进行处理的功能,任何人都可以对加密数据进行运算,运算过程不中不会泄露任何原始内容。同时,拥有密钥的用户对处理过的数据进行解密后,得到的正好是运算后的结果。
具体场景
结合区块链中的智能合约和同态加密技术,在个人征信隐私保护中,利用同态加密,设置访问权限,在不暴露个人明文信息的同时,创建与之相匹配的合约,但征信系统无法得知访问用户的需求。
强调隐私的业务,例如机构之间转账,隐藏账户余额,将用户账户余额进行加密后,通过密文之间的加减计算,进行隐秘的转账。
Paillier加密算法
Paillier算法概述
Paillier算法是公钥加密体系的一个代表算法。但是,不同于传统的公钥加密算法,Paillier 算法除了实现对数据的公钥加密,还能保证在密文上直接进行加法操作,其结果解密后与在明文上进行操作的结果一样,因此Paillier算法完全的满足密文的加法同态性。除此之外,Paillier算法还支持明文和密文的乘法操作,具有良好的同态性,相比于当前的其他同态加密更加实用。
算法流程
Paillier加密算法定义与一般公钥加密相同,主要由以下三个部分组成:
\(\mathsf{KeyGen}(\lambda) \rightarrow (pk, sk)\):密钥生成算法,由KGA运行,输入为安全参数\(\lambda\),输出为一对公钥私钥对\((pk,sk)\)。
\(\mathsf{Encrypt}(m,pk) \rightarrow CT\):加密算法,由加密方运行,输入为用户公钥\(pk\),明文空间的任一消息\(m\),输出对应密文 \(CT\)。
\(\mathsf{Decrypt}(sk,CT) \rightarrow m\):解密算法,由解密方运行,输入为解密私钥\(sk\),密文\(CT\),输出对应明文\(m\)。
同态性质
同态加密是指这样一种加密函数,对明文进行环上的加法和乘法运算再加密,与加密后对密文进行相应的运算,结果是等价的。由于这个良好的性质,人们可以委托第三方对数据进行处理而不泄露信息。具有同态性质的加密函数是指两个明文\(a、b\)满足\(Dec(En(a)⊙En(b))=a⊕b\)的加密函数。其中\(En\)是加密运算,\(Dec\)是解密运算,\(⊙、⊕\)分别对应明文和密文域上的运算。当\(⊕\)代表加法时,称该加密为加同态加密:当\(⊕\)代表乘法时,称该加密为乘同态加密。
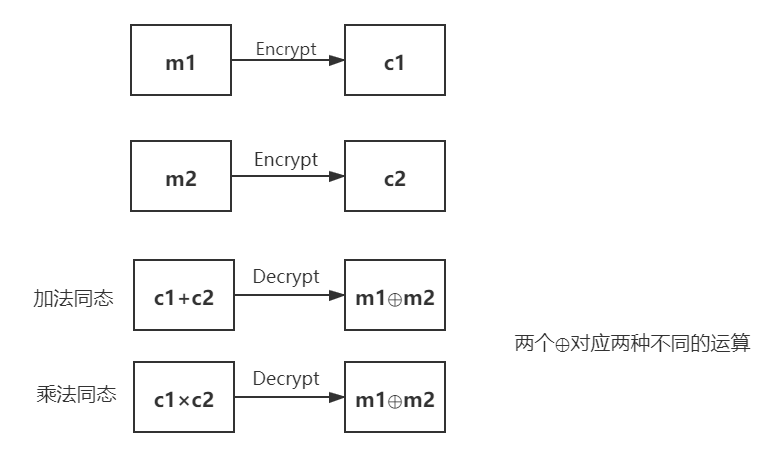
对于Paillier算法明文空间里的明文\(m_1, m_2\),Paillier加密算法具有如下同态性。
加法同态性
\(\mathsf{Encrypt}(m_1)*\mathsf{Encrypt}(m_2) = \mathsf{Encrypt}(m_1+m_2)\) ;
即,\(m_1 + m_2 = \mathsf{Decrypt}(\mathsf{Encrypt}(m_1)*\mathsf{Encrypt}(m_2))\) 。
明文和密文乘法同态性
\(\mathsf{Encrypt}(m_1)^{m_2} = \mathsf{Encrypt}(m_1*m_2)\) ;
即,\(m_1 * m_2 = \mathsf{Decrypt}(\mathsf{Encrypt}(m_1)^{m_2})\) 。
安全性分析
分析Paillier算法的加密过程,不难发现。Paillier算法,每次加密都随机选择一个随机数,这会导致同一明文两次加密会产生不同密文,这给选择明文攻击带来了不小的难度,提高了加密方案的安全性。加密算法对于保护数据安全性具有非常重要的价值,但计算复杂度也会随着算法安全性的提高而增加。
Pailier算法研究现状
研究进展
Paillier1在1999年提出了一种新的同态加密算法,即Paillier加密算法,由于Paillier算法可以进行有效的加法同态,受到了广泛的关注。2001 年,Damgard 和 Jurik 2 使用模\(n^i\)进一步对 Paillier加密体制进行了推广,并对其应用进一步推广。 Choi等人3通过选取特殊的参数\(g\),\((g^λ =1+ n\mod n^2,λ = lcm( p −1,q −1))\)改进了 Paillier加密体制。 但是Choi 等提出的变体方案不能抵抗选择密文攻击。在2006 年的欧密会上,Schoenmakers和Tuyls 4将\(x∈Z_n\)的Paillier 加密方案,扩展到了对\(x\)进行逐比特加密的Pailier加密方案。2013 年的欧密会上,Joye 和Libert 5 利用\(2^k\)阶剩余问题进一步对Paillier 加密方案进行了推广。在2014年的亚密会上,Catalano 6等等人则是提出了支持Paillier加密实例的外包密文的公开可验证授权计算方案。Castagnos Laguilaumie 7在2015年设计了一种线性同态加密方案,其安全性依赖于判定Diffie-Hellman困难问题。
同态算法对比
同态加密更具其同态完备性不同可以分为全同态和部分同态,所谓全同态就是指加密方案支持乘法和加法同态,部分同态则是指其只满足加法或者乘法同态。Paillier就是具备良好的加法同态的部分同态加密算法,除了Paillier之外,还有支持乘法同态的RSA和EIGamal算法,以及支持比特异或同态的Goldwasser Micali算法。下表1对目前经典的三种同态加密方案从计算复杂度、安全性、同态性三个方面进行了对比。
表1 经典同态算法对比
同态加密算法 |
计算复杂度 |
原理 |
安全性 |
同态性 |
|---|---|---|---|---|
Paillier算法 |
较低 |
判断复合剩余类困难性 |
强 |
加法同态、明文乘法同态 |
RSA 算法 |
较低 |
分解大素数 |
较弱 |
乘法同态 |
Gentry 算法 |
高 |
离散子集求和问题 |
强 |
加法同态,乘法同态 |
采用的paillier同态加密算法
基本概念
\(Paillier\)加密系统是一种加法同态公钥加密系统,这种加密技术已广泛应用于加密信号处理或第三方数据处理领域。其同态特性表现为:在加密后可直接对密文进行相应的算术运算,其运算结果与明文域中对应的运算结果一致。其概率特性表现为:对于相同的明文,可通过不同的加密过程得到不同的密文,从而保证了密文的语义安全。
前提假设:
随机选择两个大质数p、q满足\(gcd(pq, (p-1)*(q-1))\)。
\(计算n=p*q\)
\(g = n+1\)
\(λ = φ(n) = (p-1)*(q-1)\)
定义\(L(x) = (x-1) / n\)
\(μ = φ(n)^{-1} (mod{n})\)
公钥为\((n,g)\)
私钥为\((λ,μ)\)
算法构造:
Encryption
设\(m\)为要加密的消息,显然需要满足,\(0 \leq m < n\)
选择随机 \(r\),保证\(gcd(r, n) = 1\)
密文\(c\):\(c = (g^m) *(r^n) mod n^2\)
Decryption
\(m = ( L( c^λ mod n^2 ) * μ ) mod n\)
简化的证明过程:
由 \(L(c^λ (mod{n^2}) * μ) (mod{n})\)
有 \(L(g^{mλ}*r^{nλ} pmod{n^2}*μ) (mod{n})\) ①
其中\(λ = (p-1)*(q-1), μ = φ(n)^{-1} pmod{n}\)
∵\(r^{nλ} = r^{n(p-1)*(q-1)} = r^{φ(n^2)}\)
由欧拉定理:\(r^{φ(n^2)}\equiv1(mod{n^2})\)
①式 => \(L(g^{mλ} pmod{n^2}*μ) pmod{n}\) ②
∵\(g = n+1\)
∴\(g^{mλ} = (1+n)^{mλ} \equiv nλ+1 (mod{n^2})\)
②式=> \(L((nmλ+1)*μ) mod{n}\)
=> \(\frac{(nmλ+1)-1}{n}*μ (mod{n})\)
=>\((mλ*μ) (mod{n})\) ③
∵\(λ = φ(n),μ = φ(n)^{-1} (mod{n})\)
∴③式: \((mλ*μ) \equiv m (mod{n})\)
证毕
同态加法
两个密文的乘积解密为明文之和
\(D\left(E\left(m_{1}, r_{1}\right) \cdot E\left(m_{2}, r_{2}\right) \bmod n^{2}\right)=m_{1}+m_{2} \bmod n\)
证明
\(\begin{array}{l}D\left(E\left(m_{1}, r_{1}\right) \cdot E\left(m_{2}, r_{2}\right) \bmod n^{2}\right)=D\left(g^{m_{1}} \cdot r_{1}^{n} \cdot g^{m_{2}} \cdot r_{2}^{n}\right) \bmod n^{2}=D\left(g^{m_{1}+m_{2}} \cdot\left(r_{1} r_{2}\right)^{n}\right) \bmod n^{2}=m_{1}+m_{2}\end{array}\)
同态数乘
密文的明文次幂解密为明文的数乘
\(D\left(E\left(m_{1}, r_{1}\right)^{k} \bmod n^{2}\right)=k m_{1} \bmod n\)
证明:
\(D\left(E\left(m_{1}, r_{1}\right)^{k} \bmod n^{2}\right)=D\left(\left(g^{m_{1}} \cdot r_{1}^{n}\right)^{k}\right) \bmod n^{2}=D\left(g^{k m_{1}} \cdot r_{1}^{k} n\right) \bmod n^{2}=k m_{1} \bmod n\)
方案描述
整体架构
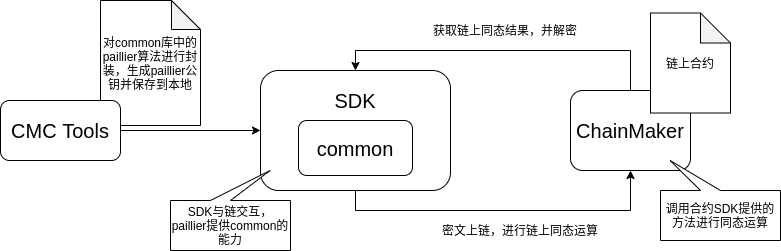
执行流程
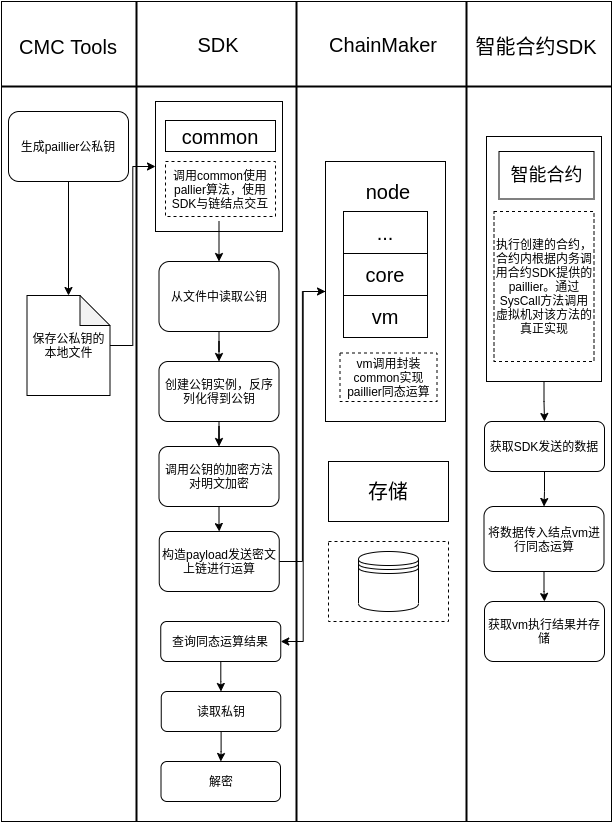
参考
[1] Paillier P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes[J]. Lecture Notes in Computer Science, 1999, 547(1):223-238.
[2] Damgård I, Jurik M. A Generalisation, a Simplication and Some Applications of Paillier’s Probabilistic Public-Key System[J]. Lecture Notes in Computer Science, 2001, 7(45):119-136.
[3] Choi D H, Choi S, Won D. Improvement of Probabilistic Public Key Cryptosystems Using Discrete Logarithm[C]. International Conference Seoul on Information Security and Cryptology. Springer-Verlag, 2001:72-80.
[4] Schoenmakers B, Tuyls P. Efficient Binary Conversion for Paillier Encrypted Values[C]. Advances in Cryptology - EUROCRYPT 2006:522-537.
[5] Joye M, Libert B. Efficient Cryptosystems from 2k-th Power Residue Symbols[M]. Advances in Cryptology – EUROCRYPT 2013. Springer Berlin Heidelberg, 2013:651-4.
[6] Catalano D, Marcedone A, Puglisi O. Authenticating Computation on Groups: New Homomorphic Primitives and Applications [M]. Advances in Cryptology – ASIACRYPT 2014. 193-212.
[7] Castagnos G, Laguillaumie F. Linearly Homomorphic Encryption from DDH [M]// Topics in Cryptology –- CT-RSA 2015. Springer International Publishing, 2015:487-505.-